Chapter 2 R的数据类型和相关计算

学过统计分析之后，我们知道统计分析最基本的就是数学计算。所以，在介绍R编程之前，我们首先来了解如何使R进行数学计算。R具有强大的计算能力。通过本章，我们可以了解：

用R进行算术运算
变量、向量(vector)、矩阵(matrix)和数组(array)、列表(list)、以及日期和时间
用R进行逻辑运算
如何使用R自带的函数进行运算

2.1 基本数据类型

我们知道计算机本来就是用来计算的数值的，就像我们上节做算术运算时用的数值。因此，数值就是R中一种数据类型。另外，计算机还可以处理文字、图像、视频、音频等等数据。

R中最基本的数据类型有：

数值:包括整数、浮点数(也是就带小数点的数)、甚至是虚数。
字符串：也就是文字，如中文的字、词、句子、一段文章，英文中的字母、单词、无意义的字母组合、句子、一段文章等等。
布尔型：只有两种取值或者状态，TRUE（真）或者FALSE（假）。
空值：学过统计，我们知道数据中会有缺失值的情况，这些缺失值就是空值。在R中，空值用NA表示，NA不是North America，而是not available（不可用的）的缩写。

2.2 变量（Variables）

变量就像一个贴着标签的抽屉。我们可以把东西放进去，可以看它里边有什么东西，可以把里边的东西替换成别的东西，但是标签上的名字不可以变。

2.2.1 变量的赋值

在R中，当我们创建或者定义一个变量时，就要给它赋一个初始值。变量的赋值就相当于把东西放进抽屉的过程。在R中，我们用赋值命令“<-”给变量赋值，也可以用等号（“=”）给变量赋值。例如我们将一个数5赋值给变量x：

x <- 5

如果要看x存储的值是什么，我们可以用print(x)或者show(x)，或者直接在控制台输入x，然后回车。

## [1] 5

字符串的变量

#这句代码可以使R打印出中文
Sys.setlocale("LC_ALL","Chinese")

## [1] "LC_COLLATE=Chinese (Simplified)_China.936;LC_CTYPE=Chinese (Simplified)_China.936;LC_MONETARY=Chinese (Simplified)_China.936;LC_NUMERIC=C;LC_TIME=Chinese (Simplified)_China.936"

str <- "少小不努力，老大徒伤悲。"
print(str)

## [1] "少小不努力，老大徒伤悲。"

布尔型变量

bool <- TRUE
bool

## [1] TRUE

空值变量

na <- NA
na

## [1] NA

我们还可以改变x的值，这就相当于将抽屉里的东西换成别的东西。不同的是，我们不需要取出x里的值再放进去，只需要给x重新赋值即可。

x = 100
x

## [1] 100

此外，函数的返回值同样可以被赋值给一个变量。后面，我们会不断地接触到这样的操作。

2.2.2 变量命名：如何给变量取名字

在R中，变量命名有三个原则：

取个有意义的名字，而不是只简单地用x，y，z，a，b，c。例如，一个变量要存储学生的姓名，我们可以给它取名为name或者xingming。这样可以增加程序的易读性，也方便我们记住变量存储的值是什么。
变量名通常可以使用字母、数字、和点（.）或者下划线（_）。但是，变量名必须以字母或者点（.）加上一个字母开头，如name或者.name。
在R中，变量名是区分大小写的，例如，name和Name是不同的。

*注意，目前R中变量命名暂不支持中文字符。

思考题：为什么我们需要变量，而不直接使用数值来进行运算？

这是因为在编程时，我们可能会在许多地方用到同样的数值，而且这些数值在不同的条件下，可能会发生变化。因此，如果我们把这个数值赋给一个变量，当数值在不同条件下发生变化时，我们只需要改变变量的赋值就可以了，而不需要在程序中每个地方改变那个数值。在后边的编程中，我们可以慢慢体会变量的好处。

2.3 算术运算

R使用键盘上常用的加（+）减（-）乘（*）除（/）的符号进行算术运算，^用来做幂运算（指数运算）。括号()用来指定运算的顺序，两个百分号（%%）用来做取模运算（求余运算，是在整数运算中求一个整数除以另一个整数的余数的运算），在两个百分号之间加一个除号（%/%）用于做整数除法，即求一个整数除以另一个整数得到结果的整数部分。下面，我们在R的控制台中一一体验一下这些运算。

#加法 +：

13 + 5

## [1] 18

#减法 -：

13 - 5

## [1] 8

#乘法 *：

13 * 5

## [1] 65

#除法 /：

13 / 5

## [1] 2.6

# 混合运算：

(13 + 5)/2

## [1] 9

#求余运算 %%：

13 %% 5

## [1] 3

#整数除法运算 %/%：

13 %/% 5

## [1] 2

#幂运算 ^：

(1 + 1/100)^100

## [1] 2.704814

2.3.1 变量在算术运算中的使用

变量创建完之后，我们就可以使用它们。变量被赋了什么值，这个变量在使用时就代表这个值。例如：

num <- 100
(1+1/num)^num

## [1] 2.704814

我们还可以在计算中使用变量之后，再将计算的结果赋值给该变量。例如：

num <- 100
num <- (1+1/num)^num
num

## [1] 2.704814

或者

num <- 1
num <- num + 1
num

## [1] 2

2.4 逻辑表达式和逻辑运算

逻辑表达式是使用比较运算符，大于（>）、小于（<）、大于等于（>=）、小于等于（<=）、等于（==）、不等于（!=），和逻辑运算符，&（与）、|（或）、非（!）、异或（xor），连接起来，并用括号()来控制运算顺序的表达式。

逻辑表达式的值是TRUE或者FALSE。数字1和0也可以分别用来表示TRUE和FALSE。

比较运算符容易理解。

比较运算符的例子

5 <= 4

## [1] FALSE

2 + 2 == 4

## [1] TRUE

7 %% 3 != 2

## [1] TRUE

我们着重解释一下逻辑运算符。

如果A或B（A|B）是TRUE，那么A和B中至少要有一个为TRUE。如果A|B是FALSE，那么A和B全部为FALSE。
如果A与B（A&B）是TRUE，那么A和B必须全为TRUE。如果A&B是FALSE，那么A和B至少有一个为FALSE。
如果A为TRUE，!A为FALSE，反之亦然。
xor(A, B)表示，如果A和B一个为TRUE，一个为FALSE，那么xor(A, B)为TRUE。如果A和B相同，那么xor(A, B)为FALSE。

逻辑运算的例子

A <- c(0, 0, 1, 1)
B <- c(0, 1, 0, 1)
#与
A&B

## [1] FALSE FALSE FALSE  TRUE

#或
A|B

## [1] FALSE  TRUE  TRUE  TRUE

#非
!A

## [1]  TRUE  TRUE FALSE FALSE

#异或
xor(A, B)

## [1] FALSE  TRUE  TRUE FALSE

2.4.1 逻辑表达式的应用

1. 从向量中提取子向量

前边我们提到过可以通过逻辑向量访问向量\(vec\)中的多个元素。被访问的元素可以作为一个子向量保存到一个变量中。这个逻辑向量的长度要和\(vec\)的长度相同。向量\(vec\)中对应逻辑向量中为TRUE的元素，被提取出来形成一个子向量。

这里，我们可以利用逻辑表达式来提取向量的子集。

例如，我们想要找到1到20的整数中能被3整除的数。

x <- 1:20

#x中的每一个数除以3余数为0，即被3整除
x %% 3 == 0

##  [1] FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE  TRUE
## [13] FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE

#用上一步生成的逻辑向量来找到1到20之间能被3整除的数
(y <- x[x %% 3 == 0])

## [1]  3  6  9 12 15 18

R也提供了一个函数subset()用来提取向量的子向量。它与通过逻辑下标来提取子向量的区别就在于处理缺失值（NA）的方法不同。函数subset()会忽略缺失值（NA），但是通过逻辑下标的提取子向量的方法会保留缺失值（NA）。

例如，我们要找到向量x中大于2的所有元素。

# 通过逻辑下标提取子向量
x <- c(1, NA, 3, 4)
x>2

## [1] FALSE    NA  TRUE  TRUE

x[x > 2]

## [1] NA  3  4

#通过函数subset提取子向量
subset(x, subset = x>2)

## [1] 3 4

2. 找到元素在向量x中的索引位置

如果我们想要找到逻辑向量中为TRUE的元素在向量x中的索引位置或下标，可以用which()。

x <- c(3,5,6,1,2,8,10)

which(x%%3 == 0)

## [1] 1 3

应用逻辑表达式时，注意四舍五入的问题（rounding error）

电子计算机中的浮点数有可能会受舍入的错误的影响。

例如，\(\sqrt(2) \times \sqrt(2) == 2\)就不成立，虽然在R中\(\sqrt(2) \times \sqrt(2)\)的结果也是2。

sqrt(2) * sqrt(2) == 2

## [1] FALSE

sqrt(2) * sqrt(2)

## [1] 2

解决这个问题，可以用函数all.equal(x, y)。

all.equal(sqrt(2) * sqrt(2), 2)

## [1] TRUE

我们可以看到，以上代码返回的是TRUE。

2.4.2 &&和||

逻辑运算符\(\&\&\)和\(||\)分别是顺序求值版的\(\&\)(与)和\(|\)(或)。

假设\(x\)和\(y\)是两个逻辑表达式。求\(x\&y\)的值之前，R要先求\(x\)和\(y\)的值，再求\(x\&y\)。然而，求\(x\&\&y\)的值时，R先求\(x\)的值，如果\(x\)是FALSE，R就直接返回FALSE，不再需要求\(y\)的值了；如果\(x\)是TRUE，R要再求\(y\)的值，然后再判断\(x\&\&y\)是TRUE还是FALSE。

同样地，求\(x||y\)的值时，R只在\(x\)是FALSE的情况下才需要求\(y\)的值。

当\(y\)没有被很好地定义时，顺序求\(x\)和\(y\)的值非常有用。

例如，我们想要知道\(xsin(1/x)\)是否等于\(0\)。

x <- 0

x * sin(1/x) == 0

## Warning in sin(1/x): NaNs produced

## [1] NA

(x == 0) | (sin(1/x) == 0)

## Warning in sin(1/x): NaNs produced

## [1] TRUE

(x == 0) | (sin(1/x) == 0)

## Warning in sin(1/x): NaNs produced

## [1] TRUE

注意，\(\&\&\)和\(||\)只可以用于标量（只有大小，没有方向的量，实际上就是实数），而\(\&\)和\(|\)可以逐一用到向量里的每一个元素上。

2.5 向量（Vector）

2.5.1 向量是什么？

在数学中，向量又被叫做几何向量或者欧几里得向量，是指欧几里得几何空间中有大小和方向的线段。

有人会问，向量不是数学中几何空间的概念吗？为什么我在R里要学这个？我们看看向量到底是什么。

在数学中，向量从零点指向空间中另一个点的一个箭头。

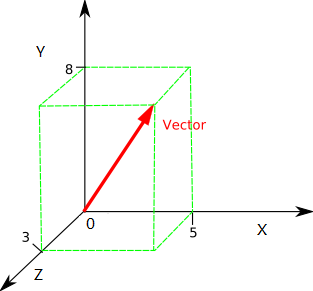
Vector

图2.1 几何空间中的向量

在上图中，三维空间中的红色向量可以用X轴、Y轴和Z轴上的投影的长度表示，即：\((5, 8, 3)\)。

如果在N维空间中呢？ N个数字表示，对不对？

\((n_1, n_2, ..., n_N)\)

向量有行向量和列向量之分，但是在R中，向量一般指的是列向量，即是一列数值。

用空间几何向量的概念解释相关系数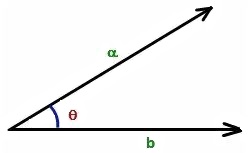

Cosine

图2.2 两个向量的相关关系

两个向量（两列数据）的相关系数其实就是这两个向量的夹角的余弦值（这里不做证明了）。

\(cor(\alpha,\ \beta)\ =\ cosine(\alpha,\ \beta)\)

2.5.2 R的向量

在R中，向量是：

一个带索引的变量（我们可以通过向量中的元素的顺序，也叫下标，作为它的索引来访问向量中的元素），
可以容纳一个及多个数值、布尔型数据、空值或字符串（它们被称为元素），
只允许相同类型的元素存在其中。

注意，c这里是小写。

首先，我们创建一个全是数字的向量\(vec\)。

vec <- c(4, 7, 6, 5, 6, 7)
vec

## [1] 4 7 6 5 6 7

接着，我们创建一个全是字符的向量\(str\_vec\)。

str_vec <- c('hello', 'world')

str_vec

## [1] "hello" "world"

当我们创建一个既有字符串又有数字的向量时，R会把数字自动升级为字符串。

mixed <- c('hello', 5)
mixed

## [1] "hello" "5"

最后，我们创建一个布尔型的向量。同时该向量中含有空值。

bool_vec <- c(TRUE, TRUE, NA, FALSE, NA, TRUE, FALSE)
bool_vec

## [1]  TRUE  TRUE    NA FALSE    NA  TRUE FALSE

2.5.3 通过下标访问向量中的元素

前面提到，我们可以通过向量的索引，或者下标，来访问向量中的元素。这个索引是元素在向量中的顺序，它是从1开始的（注意，大部分的编程语言都是从0开始的）。

访问向量中的元素

访问单个元素：向量的名字加上\([ ]\)和下标（元素的顺序，从1开始）来获得或者访问相应的元素，例如\(vec[4]\)。

vec <- c(4, 7, 6, 5, 6, 7)

vec[1]

## [1] 4

vec[5]

## [1] 6

vec[1] + vec[5]

## [1] 10

访问多个元素：
- 如果我们想访问多个元素的话，可以将我们想要访问的元素的下标放到另外一个向量里，再将这个向量放到\([]\)里, 例如\(vec[c(2, 3, 6)]\)。
- 可以去掉向量中的某些元素，用减号-加上下标向量，例如， \(vec[-c(1,4,5)]\)。
- 通过逻辑下标访问向量中的元素。首先创建一个和向量长度相同的逻辑向量，如\(c(FALSE, TRUE, TRUE, FALSE, FALSE, TRUE)\)，逻辑向量中的TRUE或者FALSE和要访问的向量中的元素一一对应，TRUE表示我们要访问的元素，FALSE表示我们不要访问的元素，例如，\(vec[c(FALSE, TRUE, TRUE, FALSE, FALSE, TRUE)]\)。

vec <- c(4, 7, 6, 5, 6, 7)

multi <- c(2, 3, 6)
#通过下标向量访问向量中的多个元素
vec[multi]

## [1] 7 6 7

vec[c(2, 3, 6)]

## [1] 7 6 7

#去掉向量vec中的第2、3、6个元素
vec[-c(1, 4, 5)]

## [1] 7 6 7

#通过逻辑下标访问向量中的元素
l <- c(FALSE, TRUE, TRUE, FALSE, FALSE, TRUE)
vec[l]

## [1] 7 6 7

如果我们知道一个数值，如何获得它在向量中的下标呢？

答案是通过which()函数。

假如，我们想知道6在向量vec中的下标：

vec <- c(4, 7, 6, 5, 6, 7)

which(vec == 6)

## [1] 3 5

从上面输出的结果，我们看到，6在向量vec中出现了两次，第一次下标是3，第二次下标是5。

若我们想知道向量vec中的最大值和最小值的下标，我们可以先求出向量的最大值和最小值，再用which()函数找出它们的位置。

vec <- c(4, 7, 6, 5, 6, 7)

#min(vec)可得到向量的最小元素
which(vec == min(vec))

## [1] 1

#max(vec)可得到向量的最大元素
which(vec == max(vec))

## [1] 2 6

2.5.4 向量的运算

向量的算术运算会分别作用于向量中的每一个元素上。

例如,

两个向量的乘法:

#两个向量中对应的元素一一相乘
vec1 <- c(1, 2, 3)
vec2 <- c(4, 5, 6)

vec1 * vec2

## [1]  4 10 18

两个向量的加法：

#两个向量中对应的元素一一相加
vec1 <- c(1, 2, 3)
vec2 <- c(4, 5, 6)

vec1 + vec2

## [1] 5 7 9

两个向量的幂运算：

#两个向量中对应的元素一一进行幂运算
vec1 <- c(1, 2, 3)
vec2 <- c(4, 5, 6)

vec2 ^ vec1

## [1]   4  25 216

两个长度（元素个数）不同的向量进行算术运算时，R会自动重复短的那个向量，直到它的长度和长向量的长度一样。

例如，

#两个向量中对应的元素一一相乘
vec1 <- c(1, 2, 3, 4)
vec2 <- c(1, 2)

vec1 + vec2

## [1] 2 4 4 6

vec1 * vec2

## [1] 1 4 3 8

vec1 ^ vec2

## [1]  1  4  3 16

当一个数(也就是一个标量)和向量进行算术运算时，

2 + c(1, 2, 3)

## [1] 3 4 5

2 * c(1, 2, 3)

## [1] 2 4 6

c(1, 2, 3)^2

## [1] 1 4 9

2.5.5 向量函数（function）

在数学中，函数是一个或者多个因变量随着一个或者多个自变量变化的一种关系。在R编程中，函数也是以类似的方式运作。函数是编程的精髓，它使得我们写出的计算机程序可以重复使用。这里，我们只是使用函数，不必深究其工作原理，后面会具体了解函数，并且要自己会写函数。

R中有许多内在的函数，如前面创建变量所用到的c()函数。我们调用或者使用函数时，只需要打出函数的名字，后边跟着括号，括号中是函数所接受的参数值。参数与参数之间需要用逗号隔开。函数执行之后会返回执行的结果。

注意：R编程中所用到的逗号和括号切换成英文状态下的逗号和括号。如果使用中文的符号，R会报错。

下面，我们举例说明如何用其他函数来创建以及操纵向量。

其他创建向量的方法

如果我们要创建一个整数或者浮点数序列，可以用操作符“:”或者函数seq()，它们返回的结果也是一个向量。

seq1 <- 1:10
seq1

##  [1]  1  2  3  4  5  6  7  8  9 10

seq2 <- seq(from=1, to=10, by=2)
seq2

## [1] 1 3 5 7 9

上面的例子中，用冒号“:”创建1到10的序列时，相邻两个数字之间的间隔只能是1。

而在使用seq()创建一个序列时，参数from和to指定序列的区间，参数by指定相邻两个数之间的间隔。

再看一个例子：

seq(0, 1, 0.2)

## [1] 0.0 0.2 0.4 0.6 0.8 1.0

注意，如果调用函数时，不加参数的名字（如，from，to，和by），函数中的参数顺序应该和其定义时的顺序一样。如果使用参数的名字，如from=1，则参数的顺序可以改变。

当调用seq()时，参数by为负数时，可以创建从大到小的序列。例如，

seq(by = -2, from=10, to=1)

## [1] 10  8  6  4  2

如果我们想要创建一个全是相同元素的向量，可以用rep()函数。

#创建一个包含5个TRUE的向量
rep_true <- rep(TRUE, 5)
rep_true

## [1] TRUE TRUE TRUE TRUE TRUE

rep_num <- rep(1, 5)
rep_num

## [1] 1 1 1 1 1

rep_str<- rep("hello", 5)
rep_str

## [1] "hello" "hello" "hello" "hello" "hello"

获得向量中元素个数

如果一个变量有许多元素，一个一个地数，不现实。我们可以用函数length()获得向量中的元素个数。

longvec <- seq(1, 147, 3)
longvec

##  [1]   1   4   7  10  13  16  19  22  25  28  31  34  37  40  43  46  49  52  55
## [20]  58  61  64  67  70  73  76  79  82  85  88  91  94  97 100 103 106 109 112
## [39] 115 118 121 124 127 130 133 136 139 142 145

length(longvec)

## [1] 49

获得向量中数据的类型

如果我们想知道一个向量中包含的值的类型是什么，用class()函数。

class(longvec)

## [1] "numeric"

mixed <- c("hello", 5)
class(mixed)

## [1] "character"

从以上的结果，我们可以看出，当把字符串和数值放到同一个向量时，数值被升格为字符串。

使用向量元素进行计算

我们还可以用函数sum()计算向量中所有元素的和，用mean()求其平均数、用median()求其中位数等。这些函数都会返回/输出一个数值，我们可以把这个数值赋值给变量。

vec <- 1:10

#求vec中所有元素的和
s <- sum(vec)
s

## [1] 55

#求vec的平均数
m <- mean(vec)
m

## [1] 5.5

#求vec的中位数
md <- median(vec)
md

## [1] 5.5

#求vec的最小值
min <- min(vec)
min

## [1] 1

#求vec的最大值
max <- max(vec)
max

## [1] 10

去掉向量中重复的元素

有的向量中有重复的元素，函数unique()和duplicated()可以帮我们去年重复的元素。

names <- c("Xiaoming","Ermao","Ermao","Xiaoming","Ermao","Zhuzi")
table(names)

## names
##    Ermao Xiaoming    Zhuzi 
##        3        2        1

从上面的结果，我们可以看到在这个names向量中“Ermao”出现了3次，“Xiaoming“出现了2次，“Zhuzi”出现了1次。

下面，我们用unique()函数去掉向量names重复的元素。

unique(names)

## [1] "Xiaoming" "Ermao"    "Zhuzi"

函数duplicated(x)返回一个逻辑向量，告诉我们向量x中哪个元素是重复的。这样，我们就可以采用逻辑下标访问向量x中不重复的元素，去年重复的，或者相反。具体操作如下：

duplicated(names)

## [1] FALSE FALSE  TRUE  TRUE  TRUE FALSE

#下边的感叹号（！）是否定的意思。逻辑向量前边加上它，向量中的TRUE就变成FALSE，FALSE就变成TRUE。
no_dup <- !duplicated(names)
no_dup

## [1]  TRUE  TRUE FALSE FALSE FALSE  TRUE

names[no_dup]

## [1] "Xiaoming" "Ermao"    "Zhuzi"

获得两个向量的交集、并集和不同的元素

setA <- c("a", "b", "c", "d", "e")
setB <- c("d", "e", "f", "g")

#两个向量的并集
union(setA,setB)

## [1] "a" "b" "c" "d" "e" "f" "g"

#两个向量的交集
intersect(setA,setB)

## [1] "d" "e"

#获得向量setA中所有不同于向量setB中的元素的元素
setdiff(setA,setB)

## [1] "a" "b" "c"

#获得向量setB中所有不同于向量setA中的元素的元素
setdiff(setB,setA)

## [1] "f" "g"

其他函数

当然，还有很多可用于向量的函数。这里有一个表包含了很多向量函数。当您需要时，可以从这里查它们的功能。

Table 2.1: 向量函数
函数	功能
max(x)	求向量x的最大值
min(x)	求向量x的最小值
sum(x)	求向量x中的所有数值的和
mean(x)	求向量x的平均值
median(x)	求向量x的中位数
range(x)	返回向量的最小值和最大值
var(x)	求向量x的样本方差
cor(x, y)	求向量x和y的相关系数
sort(x)	对向量x中的元素进行递增排序，并返回排序后的向量
rev(sort(x))	对向量x中的元素进行递减排序，并返回排序后的向量
order(x)	先将向量x中的元素升序排列，得到向量x中每个元素的位置序号，然后返回一个向量包含向量x中的每个元素的位置序号
rank(x)	计算向量的秩，并返回这个秩向量
quantile(x)	返回一个包含向量x的最小值, 25百分位数, 中位数,75百分位数, 和最大值的向量
cumsum(x)	返回一个将向量x中元素按索引顺序累加的向量，例如向量x=(1,2,3),返回向量就是（1，3，6）
cumprod(x)	返回一个将向量x中元素按索引顺序累乘的向量，例如向量x=(1,2,3),返回向量就是（1，2，6）
cummax(x)	返回一个向量，它包含到向量x中每个元素之前累积的最大值
cummin(x)	返回一个向量，它包含到向量x中每个元素之前累积的最小值
pmax(x,y,z)	返回一个向量，其长度等于向量x、y、z中最长的那个向量的长度。它包含向量x、y、z的第i个位置上元素中最大的值
pmin(x,y,z)	返回一个向量，其长度等于向量x、y、z中最长的那个向量的长度。它包含向量x、y、z的第i个位置上元素中最小的值
colMeans(x)	求dataframe x或矩阵x的每列的平均值
colSums(x)	求dataframe x或矩阵x的每列的总和
rowMeans(x)	求dataframe x或矩阵x的每行的平均值
rowSums(x)	求dataframe x或矩阵x的每行的总和

2.6 数组与矩阵

2.6.1 数组（array）

创建数组

数组是一个多维的数据类型，由array()函数创建自一个向量，由该函数的参数dim来指定其维度。

vec <- 1:24

#创建一个维度为2 ×3 × 4的三维数组
arr <- array(vec, dim = c(2, 3, 4))
arr

## , , 1
## 
##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6
## 
## , , 2
## 
##      [,1] [,2] [,3]
## [1,]    7    9   11
## [2,]    8   10   12
## 
## , , 3
## 
##      [,1] [,2] [,3]
## [1,]   13   15   17
## [2,]   14   16   18
## 
## , , 4
## 
##      [,1] [,2] [,3]
## [1,]   19   21   23
## [2,]   20   22   24

以上代码返回了4个二维数组，因为数组的第3个维度是4。

我们也可以用dim()函数来将上边的向量转化成三维数组。

vec <- 1:24

dim(vec) <- c(2, 4, 3)

vec

## , , 1
## 
##      [,1] [,2] [,3] [,4]
## [1,]    1    3    5    7
## [2,]    2    4    6    8
## 
## , , 2
## 
##      [,1] [,2] [,3] [,4]
## [1,]    9   11   13   15
## [2,]   10   12   14   16
## 
## , , 3
## 
##      [,1] [,2] [,3] [,4]
## [1,]   17   19   21   23
## [2,]   18   20   22   24

你的任务：

仔细观察以上数组创建的过程，看看向量中的元素是如何一一地被放进数组中去的。

访问数组中的元素

访问/获取数组中的元素，可以用array加上[]实现，数组中各维度的元素的位置用逗号(,)隔开。

vec <- 1:24

#创建一个维度为2 ×3 × 4的三维数组
arr <- array(vec, dim = c(2, 3, 4))
arr

## , , 1
## 
##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6
## 
## , , 2
## 
##      [,1] [,2] [,3]
## [1,]    7    9   11
## [2,]    8   10   12
## 
## , , 3
## 
##      [,1] [,2] [,3]
## [1,]   13   15   17
## [2,]   14   16   18
## 
## , , 4
## 
##      [,1] [,2] [,3]
## [1,]   19   21   23
## [2,]   20   22   24

#访问的元素在第1维的第1个位置，第2维的第2个位置，第3维的第3个位置。
arr[1, 2, 3]

## [1] 15

从上面代码返回的结果，我们可以看到，访问三维数组中的元素，要先找到数组第3维的第3个二维数组，再根据前两个维度的位置找到该元素。

另外，我们还可以访问三维数组中的二维数组和一维的行和列向量。

#访问三维数组中第三维度的第二个二维数组
arr[,,2]

##      [,1] [,2] [,3]
## [1,]    7    9   11
## [2,]    8   10   12

#访问上边的二维数组的每一行
arr[1,,2]

## [1]  7  9 11

#访问上边的二维数组的每一列
arr[,1,2]

## [1] 7 8

2.6.2 矩阵(Matrix)

电影《黑客帝国》讲述了一个年轻的网络黑客发现现实世界是由一个名为“Matrix（矩阵）”的人工智能母体控制。人类都生活在这个母体虚拟出来的世界中，有点像现在很火的元宇宙。而电影《黑客帝国》的名字就叫做The Matrix。由此可见，矩阵对于计算机的重要性。

在R中，矩阵就是一个二维的数组。函数is.matrix()可以判断一个数据类型的对象是否是矩阵。

is.matrix(arr[,,2])

## [1] TRUE

创建向量，像创建数组一样，也有两种方式。

用函数matrix()

函数matrix()通过byrow参数控制矩阵创建的方式（按列还是按行将向量中的元素放到矩阵中去），通过nrow或者ncol指定矩阵的维度。

vec <- 1:12

mat <- matrix(vec, nrow = 3)
mat

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

由以上代码返回的结果可知，默认情况下，matrix()函数是按列的方式将向量中的元素一一放入到矩阵中的。nrow=3表示创建的矩阵是3行，那肯定就是4列了，因为我们有12个元素。

如果将matrix()中的参数byrow设置为TRUE，它将一行一行地将向量中的元素放到矩阵中。仔细观察以下代码返回的结果。

vec <- 1:12

mat <- matrix(vec, byrow = TRUE, nrow = 3)
mat

##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12

在实践中，可以根据自己的需要选择矩阵的创建方式。

用函数dim()

这是创建矩阵和创建数组一样的地方。这从另一个方面印证了矩阵是二维数组。

vec <- 1:12

dim(vec) <- c(3, 4)

vec

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

#vec既是矩阵也是一个二维数组
is.matrix(vec)

## [1] TRUE

is.array(vec)

## [1] TRUE

给矩阵的行和列命名

新创建的矩阵的行和列是没有名字的。函数colnames()返回矩阵的列名向量，函数rownames()返回矩阵的行名向量。

vec <- 1:12

mat <- matrix(vec, byrow = TRUE, nrow = 3)
mat

##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12

colnames(mat)

## NULL

rownames(mat)

## NULL

因此，将一个名字向量赋值给colnames(mat)或者rownames(mat)，便可以给矩阵mat的列和行命名了。

colnames(mat) <- c("var1", "var2", "var3", "var4")
rownames(mat) <- c("participant1", "participant2", "participant3")
mat

##              var1 var2 var3 var4
## participant1    1    2    3    4
## participant2    5    6    7    8
## participant3    9   10   11   12

或者

vec <- 1:16

mat <- matrix(vec, byrow = TRUE, nrow = 4)
mat

##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12
## [4,]   13   14   15   16

colnames(mat) <- colnames(mat, do.NULL = FALSE, prefix = "var")
rownames(mat) <- rownames(mat, do.NULL = FALSE, prefix = "participant")
mat

##              var1 var2 var3 var4
## participant1    1    2    3    4
## participant2    5    6    7    8
## participant3    9   10   11   12
## participant4   13   14   15   16

或者

vec <- 1:24

mat <- matrix(vec, byrow = TRUE, nrow = 6)
mat

##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12
## [4,]   13   14   15   16
## [5,]   17   18   19   20
## [6,]   21   22   23   24

dimnames(mat) <- list(paste("participant", 1:6, sep = ""), paste("var", 1:4, sep = ""))

mat

##              var1 var2 var3 var4
## participant1    1    2    3    4
## participant2    5    6    7    8
## participant3    9   10   11   12
## participant4   13   14   15   16
## participant5   17   18   19   20
## participant6   21   22   23   24

这里用到了列表（list）和函数paste()。有兴趣的话，您可以单独试用一下paste()函数。

2.6.3 矩阵运算

使用R进行统计分析时，数据通常以数据框（data frame）的形式保存。矩阵运算的方法也可以用于数据框中的数据的运算。

矩阵加法

\(A\)和\(B\)两个矩阵相加，它们必须有相同的维度，否则R会报错。

结果矩阵\(C\)中的元素\(C_{ij}\)是\(A_{ij}\)和\(B_{ij}\)的和。

A <- matrix(c(1,2,3,4,5,6), byrow = T, nrow = 2)
A

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6

B <- matrix(c(6,5,4,3,2,1), byrow = T, nrow = 2)
B

##      [,1] [,2] [,3]
## [1,]    6    5    4
## [2,]    3    2    1

(C <- A + B)

##      [,1] [,2] [,3]
## [1,]    7    7    7
## [2,]    7    7    7

注：在R的赋值语句放到括号中，赋值后的结果会打印出来。

数值和矩阵的乘法

一个数值\(x\)乘以矩阵\(A\)的结果是\(x\)乘以\(A\)中的每一个元素。

x <- 0.1

A <- matrix(c(1,2,3,4,5,6), byrow = T, nrow = 2)

(C <- x*A)

##      [,1] [,2] [,3]
## [1,]  0.1  0.2  0.3
## [2,]  0.4  0.5  0.6

矩阵乘法

矩阵\(A\)乘以矩阵\(B\)时：

\(A\)的列数必须和\(B\)的行数相同。
矩阵相乘和数值相乘不同，要用\(\%*\%\)。
一般情况下，\(A\ \%*\%\ B\ \neq\ B\ \%*\%\ A\)。

结果矩阵\(C\)：

行数与矩阵\(A\)的行数相同，列数与矩阵\(B\)列数相同。
矩阵\(C\)的第\(i\)行第\(j\)列的元素\(C_{ij}\)由矩阵\(A\)中第\(i\)行的元素和矩阵\(B\)中第\(j\)列的元素对应相乘，再将乘积相加所得。

A <- matrix(c(1,2,3,4,5,6), byrow = T, nrow = 2)
A

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6

B <- matrix(c(6,5,4,3,2,1), byrow = T, nrow = 3)
B

##      [,1] [,2]
## [1,]    6    5
## [2,]    4    3
## [3,]    2    1

(C <- A%*%B)

##      [,1] [,2]
## [1,]   20   14
## [2,]   56   41

(D <- B%*%A)

##      [,1] [,2] [,3]
## [1,]   26   37   48
## [2,]   16   23   30
## [3,]    6    9   12

矩阵的转置

矩阵的转置是将原矩阵的行变成列得到的新矩阵，它在统计分析中是个很常用的技术。

在R中，矩阵的转置用函数t()。

A <- matrix(c(1,2,3,4,5,6), byrow = T, nrow = 2)
A

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6

#A的转置
(C <- t(A))

##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## [3,]    3    6

行列式运算

由方阵\(A\)构成的行列式为\(|A|\)。

A <- matrix(c(5,2,1,4,3,8,7,3,3), byrow = T, nrow = 3)
A

##      [,1] [,2] [,3]
## [1,]    5    2    1
## [2,]    4    3    8
## [3,]    7    3    3

det(A)

## [1] 4

2.6.4 矩阵函数

矩阵的相关的函数多是用于对矩阵中的行或列的计算。